MÉTHODE DE PAVAGE FIGURATIF
Mise en ligne gratuite de mon livre "Parcelles d'infini - Promenade au jardin d'escher"
publié aux Éditions Pour la Science, ISBN 2-84245-075-2, en 2005


Avant-propos
L’inventeur a, tout à coup, le sentiment très net
que les conceptions auxquelles il vient de parvenir (…)
existaient déjà avant d’avoir jamais été pensées dans le cerveau humain.
Louis de BROGLIE
Ma chanson n’est vraiment terminée
que lorsqu’elle a l’air de s’être faite toute seule.
Georges BRASSENS
C’est une sensation que je ressens
chaque fois que j’exécute un projet de remplissage périodique d’un plan.
Il me semble que ce n’est pas «moi» qui décide des formes
mais que ces simples taches sur lesquelles je me penche ont leur propre volonté,
que ce sont elles qui guident le mouvement de ma main.
Maurits Cornelis ESCHER
"Il y a très longtemps, je rencontrais par hasard le domaine de la division régulière de plan ; je vis une haute muraille et j’eus la prémonition qu’il devait avoir une énigme,
que quelque chose était peut-être caché derrière ce mur par-dessus lequel je grimpais avec quelque difficulté. De l’autre coté, j’atterris dans une jungle où il me fallut faire de grands efforts
pour me frayer un chemin, jusqu’au jour où - par un parcours indirect - j’arrivai à la porte, la porte ouverte des mathématiques."
…
"Je m’y promène tout seul, dans ce magnifique jardin qui n’est cependant nullement ma propriété privée et dont la porte reste ouverte à tout le monde."
Maurits Cornelis ESCHER
Remplissage périodique d’un plan
Cette méthode, extraite de mon livre «Parcelles d’infini», vous propose une promenade dans le jardin de la division régulière du plan qu’escher a exploré dans maintes directions. Ce domaine peut paraître limité si l’on en juge par le peu d’œuvres en provenant. J’espère que ce qui suit vous fera prendre conscience qu’il existe une infinité de motifs figuratifs possibles. Et que ce n’est pas copier escher que de faire une division périodique du plan.
… Pas plus que ce n’est copier Jean-Pélerin * que de faire un dessin en perspective.
Et si, comme je le souhaite, l’envie vous prend de réaliser des «pavés» figuratifs, vous trouverez, au fil des pages, comment leur donner naissance.
Et quand, après quelques difficultés, vous en aurez réussi un, vous éprouverez un grand sentiment de joie et d’humilité devant cette «PARCELLE D’INFINI».

*. Dit le Viator. On lui doit le premier traité de perspective imprimé paru en 1505.

1 IMITER LA NATURE
Il y a tant d’art dans la nature
que l’art même ne consiste qu’à bien l’entendre et à l’imiter.
Jacques Bénigne BOSSUET
C’est une triste chose de penser que la nature parle
et que le genre humain n’écoute pas.
Victor HUGO
 es lois de hommes sont éphémères, celles de la
nature sont éternelles. Même si nos incursions sur ses chemins seront toujours modestes, cela reste une grande joie et un grand honneur que de pouvoir imaginer des
variations planes sur ses propres canevas.
es lois de hommes sont éphémères, celles de la
nature sont éternelles. Même si nos incursions sur ses chemins seront toujours modestes, cela reste une grande joie et un grand honneur que de pouvoir imaginer des
variations planes sur ses propres canevas.Les rayons des abeilles, les écailles des poissons ou les tournesols nous donnent de beaux exemples de pavage mais ce sont surtout les cristaux que la nature nous offre pour nous montrer la voie. On trouve dans leur structure les 17 groupes de symétrie permettant de répéter un motif à l’infini. Mais pour dessiner des pavages figuratifs il est préférable de nous créer une classification à la fois plus simple et plus adaptée. C’est ce que nous allons faire.

Il n’y a que trois polygones réguliers pouvant diviser périodiquement le plan, ce sont :
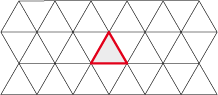
Le triangle

Le carré
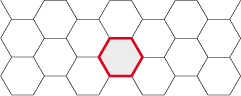
L'hexagone
Mais, par bonheur, quantités de polygones irréguliers peuvent également diviser périodiquement le plan.
Quelques exemples :
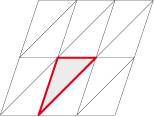
Le triangle quelconque
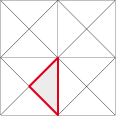
Le triangle rectangle isocèle
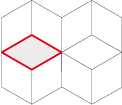
Le losange 2 angles de 120°
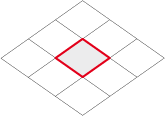
Le losange quelconque
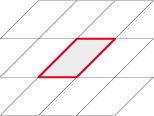
Le parallélogramme
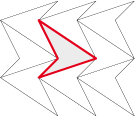
Le quadrilatère quelconque
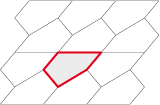
Le pentagone 2 côtés
parallèles et égaux
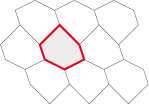
L'hexagone 2 côtés opposés
parallèles
et égaux entre 2 fois
2 côtés adjacents et égaux
De plus, il est possible de remplacer les côtés de tous les polygones divisant périodiquement le plan, par des déformations compensées ne
modifiant pas leur surface.
Exemples :

Translations de déformations compensées sur parallélo-gramme
Translations de déformations compensées sur hexagone ayant ses côtés opposés parallèles

La multiplicité des déformations compensées réalisables apporte l’étonnante possibilité de donner naissance à une infinité de motifs
figuratifs.
Exemples :
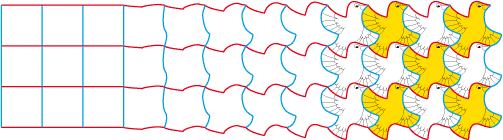
Translations progressives de déformations compensées sur carrés
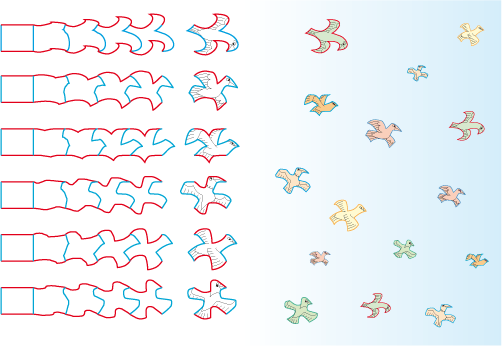
Transformations par translations d'un même rectangle en six oiseaux différents
Le polygone de base ayant subi les déformations compensées se nomme pavé.
Exemples :
• Translations sur un parallélogramme :

Polygone de base
Déformations compensées
Pavé
• Translations sur un carré :
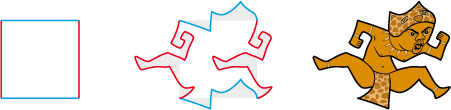
Polygone de base
Déformations compensées
Pavé
• Translations sur un hexagone concave :
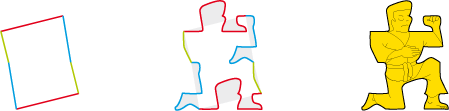
Polygone de base
Déformations compensées
Pavé
• Translations sur un hexagone régulier :
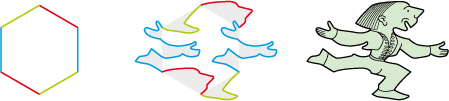
Polygone de base
Déformations compensées
Pavé
Un papier quadrillé facilite le traçage du pavé.
Exemple :
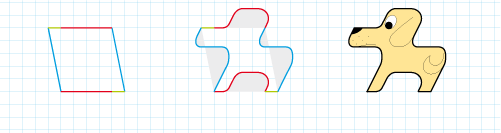
Polygone de base. Il s'agit pour
nous d'un hexagone dont 2 x 2
côtés sont en prolongement
Déformations compensées
Pavé
Un ensemble de pavés se nomme pavage :

Lucky Blanchepatte, mon cher chien disparu

2 TRANSFORMER LES POLYGONES
La géométrie est aux arts plastiques
ce que la grammaire est à l’art de l’écrivain.
Guillaume APOLLINAIRE
Plus l’art est contrôlé, limité, travaillé
et plus il est libre.
Igor STRAVINSKY
 ssayer de donner naissance à des motifs figuratifs sans bases géométriques
donne des résultats très limités. Les polygones sont les œufs desquels vont éclore une multitude de personnages.
ssayer de donner naissance à des motifs figuratifs sans bases géométriques
donne des résultats très limités. Les polygones sont les œufs desquels vont éclore une multitude de personnages.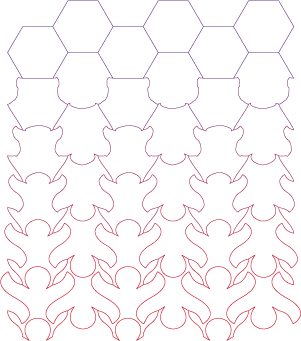

Il y a trois déformations possibles pouvant remplacer les côtés d’un polygone :
1. Quelconque (comme son nom l’indique) :
côté de polygone avant déformation
côté de polygone après déformation
axe de symétrie
centre de rotation

2. Axiale (déformation quelconque plus sa réflexion par rapport à un axe) :
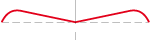
3. Rotatoire (déformation quelconque plus sa rotation à 180°) :

La déformation quelconque ou axiale d’un côté devra toujours être compensée par une déformation identique sur un autre côté. La déformation rotatoire se compense elle-même. On nomme ces compensations isométries.
Il y a quatre types d'isométries :
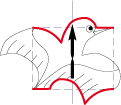
1. La translation est le simple glissement rectiligne d’une déformation :
2. La rotation est, soit une déformation rotatoire, soit le pivotement d’une déformation autour d’un centre de rotation
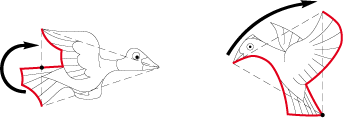

3. La réflexion glissée est la réflexion d’une déformation par rapport à un axe, suivie d’une translation :
4. La symétrie est la réflexion d’une déformation par rapport à un axe :
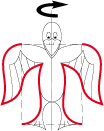
Exemples :
• Deux translations sur parallélogramme :

• Une rotation à 180° et une autre à 60°sur triangle équilatéral :

• Une réflexion glissée ainsi qu'une translation sur parallélogramme :

• Deux réflexions glissées symétriques et une translation axiale sur hexagone :

La réflexion glissée nécessite quelques précisions :
- Les côtés du polygone peuvent être adjacents (avoir une extrémité commune) ou non-adjacents :
Un polygone peut posséder deux réflexions glissées. Dans ce cas, leurs axes vecteurs sont soit parallèles soit perpendiculaires :
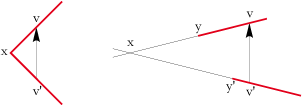
| adjacents | non-adjacents |
| Parallèles | perpendiculaires |
Le tracé des
réflexions glissées
est particulièrement
simplifié sur une
feuille de papier
quadrillé
Soit L la longueur des côtés du polygone :

Les points v et v’ permettent de tracer l’axe vecteur des réflexions glissées. Cet axe vecteur indique l’axe de réflexion ainsi que la direction et la longueur du glissement.
Exemple :

Le polygone de base de cet oiseau est un pentagone concave possédant un côté rotatoire et deux fois deux côtés d’axes vecteurs perpendiculaires.

ISOMÉTRIES
| DÉSIGNATIONS ET ABRÉVIATIONS | CONDITIONS DANS LE POLYGONE | REPRÉSENTATIONS SIMPLIFIÉS |
| La translation | T | 2 côtés parallèles et égaux |
La rotation | ||
- 180° | R2 | 1 côté quelconque |
- 120° | R3 | 2 côtés égaux adjacents à 120° |
- 90° | R4 | 2 côtés égaux adjacents à 90° |
- 60° | R6 | 2 côtés égaux adjacents à 60° |
La réflexion glissée (Si il y en a 2 dans le polygone, on rajoute ' pour la 2e) |
G | 2 côtés égaux |
La symétrie | S | 2 côtés symétriques |
Il y a quatre types de polygones pouvant diviser périodiquement le plan :

| le triangle | le quadrilatère | le pentagone | l'hexagone |
La recherche systématique de toutes les combinaisons possibles entre les quatre isométries et les quatre types de polygones permet d’aboutir à une grande quantité de polygones
spécifiques dont on élimine ceux ne pouvant pas remplir le plan.
Exemples :
Il reste alors 81 polygones spécifiques, appelés pavés isoédriques, desquels on élimine aussi ceux dont les possibilités d’obtention de motif figuratif sont trop réduites :
- car ayant un ou plusieurs bords rectilignes :
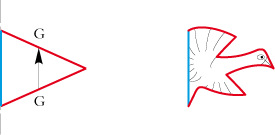
retenu car
éliminé car
- car ayant une symétrie centrale :
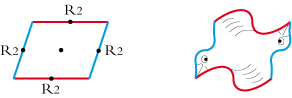
En fin de compte, il reste 35 pavés modulables ; 35 parcelles d’infini, que le magicien qui sommeille peut-être en vous, va transformer en lapin, en papillon ou en colombe.

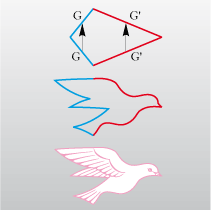
La nécessité de mettre un cadre à cette méthode ne doit pas faire oublier qu’il y a toujours des possibilités de sortir du cadre.
Exemples :
• Le splendide «chinois» d’escher possède deux côtés rectilignes :
• Demi-tour de carte possède un axe de rotation central :
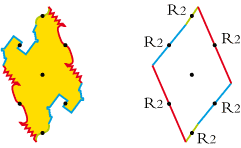

Voici son polygone de base :
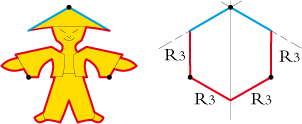

• De même pour la pieuvre
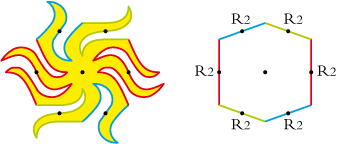

3 ASSEMBLER LES PAVÉS
Il arrive parfois qu’une personne (…)
sente naître et se développer en elle, un jour,
un désir très conscient d’approcher par l’imagination,
l’infini le plus près possible
et de
la manière la plus pure.
Maurits Cornelis ESCHER
N’espère rien de l’homme
s’il travaille pour sa propre vie et non pour l’éternité.
Antoine de SAINT-EXUPÉRY
Le sentiment de l’infini
est le véritable attribut de l’homme.
Madame de STAËL
 ssembler les pavés, c’est disposer des parcelles d’infini sur des trames
éternelles. Assembler les pavés, c’est le privilège de jouer au puzzle avec l’univers.
ssembler les pavés, c’est disposer des parcelles d’infini sur des trames
éternelles. Assembler les pavés, c’est le privilège de jouer au puzzle avec l’univers.

Des pavés semblables à un pavé modulable peuvent s’emboîter sur lui après rotation et/ou réflexion glissée. Ils ont alors une
orientation différente.
Exemples :
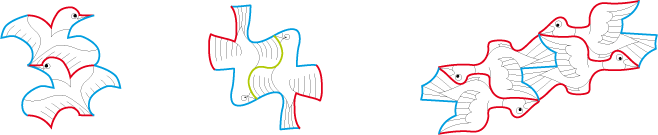
| Réflexion glissée | Rotation | Réflexion glissée + rotation |
Puis cet ensemble de pavés peut à son tour s’emboîter sur son semblable par translation, et ceci peut être continué jusqu’à l’infini :
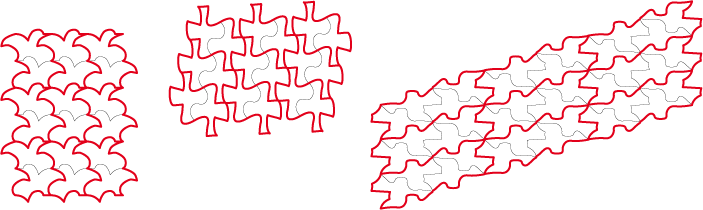
| Type 1G | Type 2 | Type 2G |
Tous ces pavés semblables sont les transformées du pavé modulable de base. L’ensemble, nous l’avons vu, se nomme pavage.

Cette ronde d’amoureux ne demande qu’à s’agrandir !
Visuellement, ce qui caractérise en premier lieu un pavage est le nombre de directions prises par ses motifs. Il y a six directions possibles, il y aura donc six types de départ.
Le type 1 aura tous ces pavés dans la même direction. Le type 2 aura ses pavés tête-bêche. Le type 3 aura ses pavés dans trois directions,
le type 4 dans quatre directions et le type 6 dans six directions.
Exemples :
• Type 1, l'athlète :
• Type 3, le lézard :

• Type 4, le chaton :


• Type 2, la sirène :
• Type 6, l'otarie :


Ensuite, les pavages à une ou deux directions peuvent avoir leurs motifs réfléchis. Il y aura donc également un type 1G (G pour réflexion Glissée) et un type 2G.
• Type 1G, le coq :
• Type 2G, le chien :


Enfin, les pavages de types 1, 2, 3 et 4 peuvent avoir leurs motifs symétriques. Nous aurons donc en plus le type 1S, le type 2S, le type 3S et le type 4S.
• Type 1S, le gorille :
• Type 2S, le papillon :


• Type 3S, le canard :
• Type 4S, la rainette :


Soit en tout 11 types qui vont se retrouver sur 11 canevas. De plus, ces 11 types possèdent des sous-types classés selon leur polygone de base. Au total nous retrouvons les 35 pavés modulables du chapitre précédent.
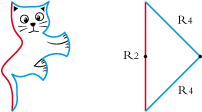
• Le polygone de base du chaton est un triangle rectangle isocèle. On le désignera par les isométries de ses côtés, soit R2 R4 R4 :
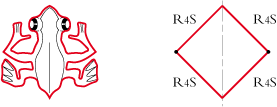
• Quand à celui de la rainette, c’est un carré. Désignation R4S R4S R4S R4S :
Voici maintenant les désignations des polygones de base pour :
• l'athlète : T T T T T T
• la sirène : R2 R2 R2
• le lézard : R3 R3 R3 R3
• l'otarie : R2 R6 R6
• le coq : T G T G
• le chien : R2 G G
• le gorille : T GS GS T GS GS
• le papillon : T R2S R2S T R2S R2S
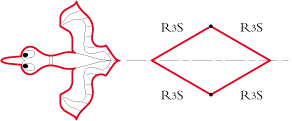
• Celui du canard est un losange ayant deux angles de 120°. Nous le désignerons par R3S R3S R3S R3S car les côtés sont à la fois des rotations 3 et des symétries :
Le polygone de base du «fou» est un hexagone régulier. Désignation R3 R3 R3 R3 R3 R3 :
L’utilisation de papier triangulé s’avère indispensable pour le
traçage des pavés possédant des isométries de rotation 3 ou 6.
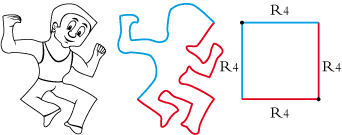
• Le polygone de base du « p’tit costaud » est un carré. On le désigne par R4 R4 R4 R4.
• Celui d’escher (eh oui ! même le profil d’escher est un pavé !) est un hexagone. Désignation T R2 R2 T R2 R2.
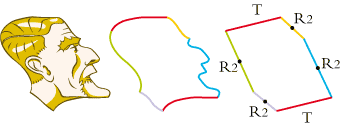



4 TISSER LES CANEVAS
S'il n'y a pas de truc, c'est fort …
S'il y a un truc, c'est encore plus fort !
MYR et MYROSKA
Toutes les choses, proches ou lointaines,
secrètement sont reliées les unes aux autres
et tu ne peux pas toucher une fleur sans déranger une étoile.
Francis Joseph THOMPSON
 es canevas sont semblables aux coulisses des théâtres de magie,
en cela qu’elles renferment tous les secrets nécessaires à la représentation. Connaître ces secrets ne désenchante que le sot.
es canevas sont semblables aux coulisses des théâtres de magie,
en cela qu’elles renferment tous les secrets nécessaires à la représentation. Connaître ces secrets ne désenchante que le sot.

Nous avons vu qu’il y a 11 canevas, mais les cristallographes dénombrent 17 groupes de symétrie. En fait, les six groupes manquants ne permettent pas de créer des motifs uniques. Nous les
indiquerons quand même après les 11 canevas.
Les canevas sont représentés à l’aide des éléments suivants :
- centre de rotation : •
- axe de symétrie : ———— — ——— — ———
- axe
de réflexion glissée : ——————————
| TYPE 2G (pgg) Rotation 180° + réflexion glissée + translation | Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
b (IH53) Quadrilatère R2 R2 G G
36 / 412 / 77 / 98 / 116
Le groupe de symétrie utilisé est celui des Tables internationales de la cristallographie des rayons X.
Le type isoédrique est celui défini par
B. Grünbaum et G. C. Shephard dans leur livre Tilings and Patterns.
Lorsque l’on a plusieurs sortes de transformées avant translations comme dans le cas présent, on
exécute d’abord la première : ce qui nous donne deux pavés. Puis nous faisons :
- soit la transformée des deux pavés ensembles (exemple du haut);
- soit la transformée de chacun des deux pavés séparément (exemple du bas avec des pavés concaves).
Les petits chiffres indiquent l'angle de rotation (2 = 180°, 3 = 120°, 4 = 90°, 6 = 60°).
Le canevas du type 1 sera absent car il ne comporte que des translations.
Dix-neuf polygones de base peuvent être concaves. Ce sont : 1b, 1Gb, 1Gc, 1Gd, 1Sb, 2b, 2d, 2e, 2Gb, 2Gc, 2Ge, 2Gf, 2Gg, 2Gh, 2Sb, 2Sc, 3b, 4c et 6d. Exemple :
Les chiffres indiquent le nombre de sommets adjacents.
Les 35 types de pavages seront représentés par 35 oiseaux.
Tous les pavages isoédriques peuvent être coloriés avec un minimum de deux ou trois couleurs. Si tous les sommets adjacents sont en nombres pairs, deux couleurs suffisent. S'il y a des sommets en nombres impairs, trois couleurs sont nécessaires.
| TYPE 1 (p1) Translations |
Canevas + polygone de base avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH41) Parallélogramme T T T T
38 / 472 / 482 / 492 / 502
/ 522 / 73 / 74 / 80 / 105 / 106 / 127 / 128
b (IH1) Hexagone T T T T T T
182 / 222 / 272 / 282
/ 292 / 302 / 722 / 822 / 842 / 872 / 922 / 1112 / 1122 / 1132
/ 1142 / 1202 / 1212 / 1292
| TYPE 1G (pg) Réflexion glissée + translations |
Canevas + polygone de base et sa transformée avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH43) Parallélogramme T G T G
31 / 32 / 7112 / 97 / 108 / 109
b (IH44) Cerf-volant * G G G' G'
19 / 62 / 66 / 67 / 762 / 96 / 102 / A13
*. Un cerf-volant est un quadrilatère convexe dont une diagonale est perpendiculaire à l'autre en son milieu.
c (IH2) Hexagone T G G T G' G'
242 / 262 / 78 / 1102 / 1262 / 1302
d (IH3) Hexagone T G G' T G' G
17 / 342 / 612 / 632
| TYPE 1S (cm) Translations |
Canevas + polygone de base avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH68) Losange GS GS G'S G'S *
91 / A14
*. Les côtés avec réflexion glissée étant symétriques, ce sont donc également et obligatoirement des translations.
b (IH12) Hexagone T GS GS T G'S G'S *
A1
*. Les côtés avec réflexion glissée étant symétriques, ce sont donc également et obligatoirement des translations.
| TYPE 2 (p2) Rotation 180° + translations |
Canevas + polygone de base et sa transformée avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH84) Triangle R2 R2 R2
51 / 95
b (IH46) Quadrilatère R2 R2 R2 R2
9 / 88 / 90 / 93
c (IH47) Parallélogramme T R2 T R2
75 / 1152
d (IH23) Pentagone T R2 T R2 R2
escher n'a pas fait de pavage de ce type
e (IH4) Hexagone T R2 R2 T R2 R2
1 / 5 / 6 / 7 / 8 / 11 / A12
| TYPE 2G (pgg) Rotation 180° + réflexion glissée + translations |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH86) Triangle isocèle R2 G G
escher n'a pas fait de pavage de ce type
b (IH53) Quadrilatère R2 R2 G G
36 / 412 / 77 / 98 / 116
c (IH51) Quadrilatère R2 G R2 G
33 / 107 / 124
d (IH52) Rectangle G G' G G'
39 / 682
e (IH25) Pentagone T R2 T G G
f (IH27) Pentagone R2 G G' G G'
16 / 462 / 592 / 602
g (IH5) Hexagone T R2 R2 T G G
10 / 582
h (IH6) Hexagone R2 G R2 G' G G'
2
| TYPE 2S (pmg) Rotation 180° + translations |
Canevas + polygone de base et sa transformée avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH66) Rectangle T R2S T R2S *
40 / 117
*. Les côtés de rotations 2 étant symétriques, ce sont donc également et obligatoirement des réflexions glissées.
b (IH69) Cerf-volant R2S R2S R2S R2S *
37 / 89
*. Les côtés de rotations 2 étant symétriques, ce sont donc également et obligatoirement des réflexions glissées.
c (IH13) Hexagone T R2S R2S T R2S R2S *
escher n'a pas fait de pavage de ce type
*. Les côtés de rotations 2 étant symétriques, ce sont donc également et obligatoirement des réflexions glissées.
| TYPE 3 (p3) 2 rotations 120° + translations |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH33) Losange R3 R3 R3 R3
escher n'a pas fait de pavage de ce type
b (IH7) Hexagone R3 R3 R3 R3 R3 R3
21 / 25 / 432
| TYPE 3S (p31m) 2 rotations 120° + translations |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH36) Losange R3S R3S R3S R3S *
532 / 542 / 103 / 123
*. Les côtés de rotations 3 étant symétriques, ce sont donc également et obligatoirement des réflexions glissées.
| TYPE 4 (p4) 3 rotations 90° + translations |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH79) Triangle rectangle isocèle R2 R4 R4
35 / 118 / 119
b (IH55) Carré R4 R4 R4 R4
15 / 23 / 104
c (IH28) Pentagone R2 R4 R4 R4 R4
14 / 20 / 423,5
| TYPE 4S (p4g) 3 rotations 90° + translations |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH71) Carré R4S R4S R4S R4S*
13 / 452 / 86 / 122 / 125
*. Les côtés de rotations 4 étant symétriques, ce sont donc également et obligatoirement des réflexions glissées.
| TYPE 6 (p6) Rotations 180°° + 2 rotations 120° + translat. |
Canevas + polygone de base et ses transformées avant translations | Exemple de pavé de base | Exemple de pavé figuratif | Exemple de pavage fléché et colorié (minimum de couleurs) |
a (IH88) Triangle équilatéral R2 R6 R6
44 / 94 / 99 / 100
b (IH39) Triangle isocèle R2 R3 R3
escher n'a pas fait de pavage de ce type
c (IH31) Cerf-volant R3 R3 R6 R6
55 / 56
c (IH21) Pentagone R2 R3 R3 R6 R6
572 / 70 / 79
Les six groupes de symétrie ne permettant pas de faire des motifs uniques :
| Désignation | Canevas | Exemple de motif figuratif | Désignation | Canevas | Exemple de motif figuratif |
pm
(2 motifs
minimum)
p3m1
(3 motifs
minimum)
cmm
(2 motifs
minimum)
p4m
(3 motifs
minimum)
pmm
(3 motifs
minimum)
p6m
(3 motifs
minimum)
les 35
polygones
de base

5 UTILISER LES POLYGONES DE BASE
L'imagination est plus importante que le savoir.
Albert EINSTEIN
La raison, c'est l'intelligence en exercice;
l'imagination, c'est l'intelligence en érection.
Victor HUGO
 ous avez la plume et le parchemin. Vous venez de prendre connaissance
des secrets des canevas. Il vous faut maintenant faire appel au plus important : votre imagination. Si, sur un vieux mur à moitié décrépi, vous voyez apparaître des figures plus ou moins fantastiques,
vous avez bon espoir de réussir.
ous avez la plume et le parchemin. Vous venez de prendre connaissance
des secrets des canevas. Il vous faut maintenant faire appel au plus important : votre imagination. Si, sur un vieux mur à moitié décrépi, vous voyez apparaître des figures plus ou moins fantastiques,
vous avez bon espoir de réussir.Vous pouvez vous en remettre au hasard pour choisir un polygone de base et tracer des déformations compensées jusqu’à ce que vous obteniez une ébauche de motif. Ou vous pouvez déjà avoir
une idée du motif à dessiner, le tracer en gros, y adapter le type de polygone de base convenant le mieux et reprendre les déformations compensées.
Bien sûr, il vous faudra utiliser beaucoup la gomme avant de réussir un pavé figuratif.
Souvent votre motif ne sera qu’à moitié réussi et il vous faudra recommencer.
Mais si vraiment vous n’obtenez rien de satisfaisant, tout n’est pas perdu. À l’aide de votre ordinateur, retracez votre pavé raté. À l’intérieur de votre pavé ajoutez quelques motifs sans rapport,
puis sélectionnez le tout et donnez un fond dégradé à tous ces tracés, dans le style arc-en-ciel ou couché de soleil tropical. Il ne vous reste plus qu’à baptiser l’ensemble d’un nom idiot et vous
venez de créer un digne représentant de l’art abstrait !

Maintenant que vous connaissez comment fonctionnent les canevas, le résumé des 35 polygones de base précèdent va vous aider à donner naissance à des pavés figuratifs. Votre matériel : du papier quadrillé, du papier triangulé pour les types 3 et 6, un crayon et une gomme. C’est tout ! Quand vous voudrez multiplier les pavés pour faire des pavages, un ordinateur avec un programme de dessin sera bien commode. Mais pas indispensable, n’oubliez pas qu’escher a gravé tous ses pavages à la main. Un logiciel de pavage comme celui de Kevin Lee (TesselManiac) vous apportera aussi une aide précieuse pour la création de pavés.
Hexus
(Art abstrait !) type 1b
Coude à coude
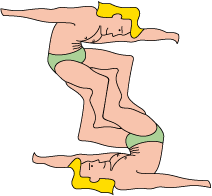
Antipodistes icariens impossibles
type 2c

Contresens

Le Sommeil de Samson
(Art moderne !) type 2c

Attention … sapin !

Jaloux
Après ce petit intermède de pavés plus ou moins réussis, revenons à nos polygones de base.
• Prenons un carré de type 1Ga. Traçons quelques lignes brisées sur deux côtés adjacents (a). Puis repportons-les sur les deux autres côtés à l’aide d’une translation et d’une réflexion glissée (b). Étudions la figure ainsi formée : elle a vaguement une allure de bonhomme. Diminuons le bras gauche, cela augmente le bras droit (c) :
Modifions la jambe gauche, cela améliore le bras droit et la jambe droite (d). Travaillons les détails extérieurs en tenant compte à la fois de ce que serait le tracé idéal d’un côté et de ce que serait celui de son isométrie (e). Maintenant traçons les détails intérieurs du bonhomme. On s’aperçoit alors que l’on peut encore améliorer certains tracés extérieurs (f) :
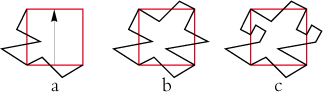
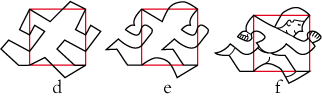
Rendez-vous compte de ce que nous venons de faire : nous avons transformé un rigide carré en un jeune garçon qui court gaiement sur notre feuille de papier !
• Prenons maintenant un rectangle, toujours du type 1Ga, et traçons quelques lignes. Nous obtenons bientôt le contour d’un militaire en train de défiler :
Mais sa silhouette est penchée en avant. Transformer le rectangle de base en un parallélogramme va nous permettre de la redresser :
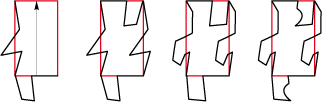
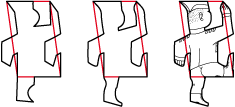
Et voici, d’un rectangle au départ, nous obtenons un vaillant militaire qui défile fièrement plus bas.
• En fait, bon nombre de dessins de pavés figuratifs ont commencé par être … des dessins ! Prenons par exemple la chèvre ci-dessous. Examinons-la. Il apparait évident qu’il y a une possibilité de réflexion glissée entre les pattes de devant et les cornes :
Puis peut-être une autre entre une patte arrière et la queue. Il ne reste plus qu’à adapter les réflexions glissées dans un cerf-volant de type 1Gb.
Et voilà une brave petite chèvre qui descend de la montagne ci-dessous :
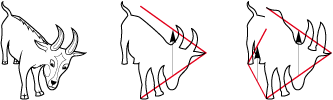
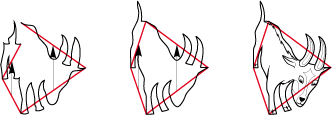
Après ces trois exemples, peut-être cele vous parait-il facile de dessiner des motifs figuratifs. Détrompez-vous, il vous faudra essayer et essayer encore, cent fois sur le métier remettre votre ouvrage.
• Reprenons un carré de type 1Ga et essayons quelques ligne. Après tranformation du carré en rectangle puis en parallélogramme apparait un indien, la main levée en signe de paix :
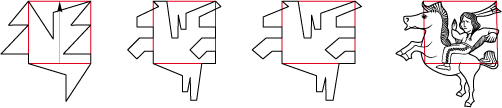
• Après les indiens, voici les cow-boys avec pour polygone de base un hexagone de type 1Gc :
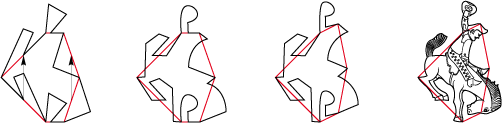
• Retrouvons la silhouette mythique du cow-boy de rodeo dans un hexagone concave de type 1Gd :

Vous remarquerez que le chapeau est détaché du cavalier et de son cheval. Nous avons là, en fait, un pavé composé de deux sous-pavés (voir chapitre Diviser les pavés).
• Restons en Amérique avec le créateur du rockabilly, Elvis lui-même, dans son hexagone régulier de type 1Gc :
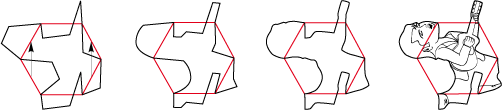
• Le losange de type 1Sa peut faire apparaître la silhouette d’un ours :

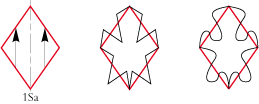
• Mais si l’on penche l’ours, le losange se transforme en un parallélogramme de type 1a :

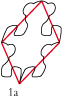
• Et, si l’ours se met à danser, le polygone de base devient un cerf-volant de type 1Gb :

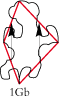
• Le rectangle de type 2Gd se transforme facilement en un poisson ondulant et pourrais faire un joli carrelage de salle de bain :

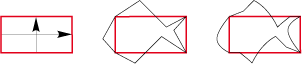

• D’un triangle pointu de type 2a naissent les jolies courbes d’une naïade :
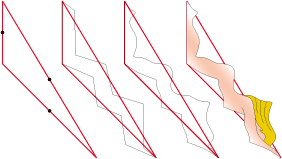
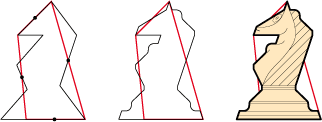
• Ce cheval de jeu d’échec s’est développé à partir d’un quadrilatère de type 2b :
• Ce bon gros père remplit très bien un hexagone de type 2Sc :
• Ce parallélogramme de type 2b se transforme en un quadrilatère quelconque pour révéler un judoka en pleine action :
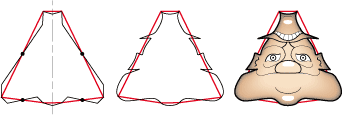
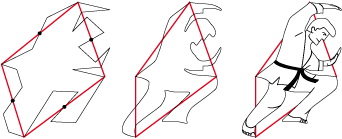
Mais il a peut-être une face cachée …
• En pleine action également ce singe acrobate issu d’un pentagone concave de type 2Ge :
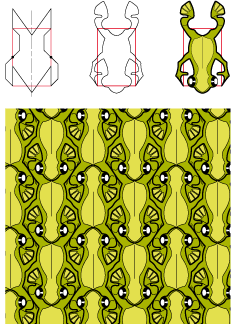
• Un hexagone de type 2Gg est à la base du poisson ci-dessous. Mais seulement de ses contours car les détails de la moitié des poissons - qui devraient être à l’envers - ont été dessiné à l’endroit :
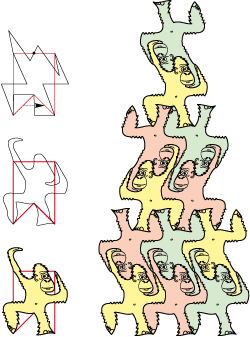
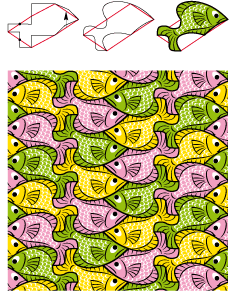

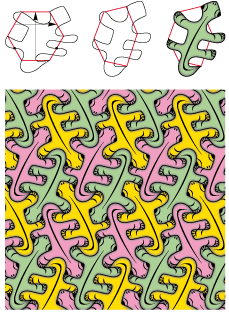
• Ce lézard gonflable est très pratique pour être rangé sur la plage. Son polygone de base est un hexagone de type 2Gh :
• La rainette peut aller et venir dans un rectangle de type 2Sa :
• Si l’on excepte ses nageoires ventrales, le scalaire s’adapte parfaitement a un cerf-volant de type 2Sb :
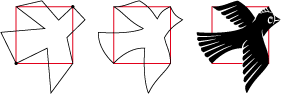
• Ce carré de type 4b peut donner naissance à un oiseau huppé :
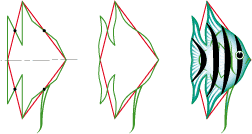

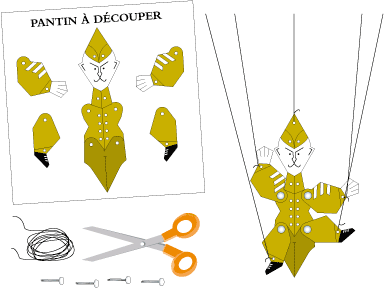
• Vous pouvez découper le pantin ci-dessous et l’assembler :
Peut-être remarquez-vous qu’avec les bras et les jambes en l’air celui-ci peut également être issu d’un losange de type 3Sa. Ainsi nous pouvons dessiner ses transformées et nous constituer une armée de pantins !


6 DIVISER LES PAVÉS
On ne se distrait jamais si bien qu'à la poursuite de l'éternité.
Jean GIONO
Si tu veux progresser vers l'infini,
explore le fini dans toutes les directions.
Johann Wolfgang von GOETHE
 es cellules se divisent pour se multiplier : pourquoi les pavés n’en
feraient-ils pas autant pour s’en aller deux par deux, voir trois par trois ou même plus, paver l’infini ?
es cellules se divisent pour se multiplier : pourquoi les pavés n’en
feraient-ils pas autant pour s’en aller deux par deux, voir trois par trois ou même plus, paver l’infini ?Le pavage avec cet hexagone donnera la figure ci-dessous. Trois couleurs sont nécessaires :


Les pavés de tous les types que nous avons vus peuvent être divisés en autant de sous-pavés que nous le désirons.
Prenons par exemple un hexagone à côtés opposés parallèles du type 1b :

Divisons cet hexagone de plusieurs façons :
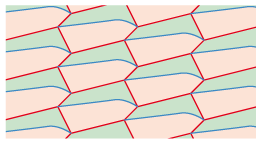
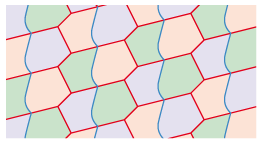
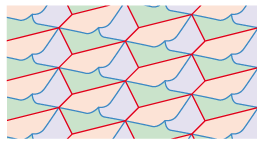
En fait nous pouvons diviser le pavé de base en autant de façons différentes que nous le souhaitons.
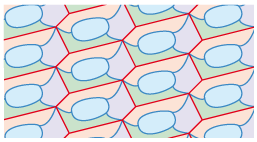
Diviser entraîne des changements dans les sommets, donc dans le nombre de
couleurs minimum. Nous avons vu que, si tous les sommets adjacents d’un pavage isoédrique sont en nombres pairs, deux couleurs suffisent, et que s’il y a des sommets en nombres impairs,
trois couleurs sont nécessaires. Il n’en est pas de même pour les sous-pavés qui peuvent nécessiter jusqu’à quatre couleurs.
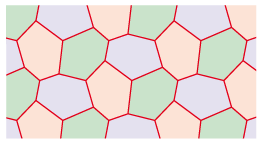
| Exemple type 1b | Exemple type 3b |
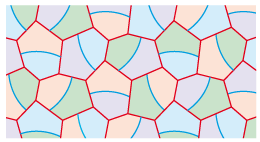
• Voici un pavé du type 2Gc qui ne ressemble pas à grand chose :
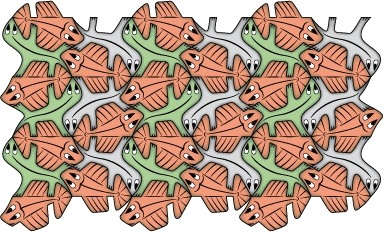
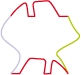
Mais sa division en deux laisse apparaître un poisson et un lézard :
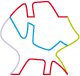
• Lors d’une promenade,ramassez une feuille d’arbre. Dessinez-en le contour :
Copiez-en une troisième et une quatrième toujours en faisant coïncider un autre sommet :
Avec un calque dessinez une deuxième feuille en faisant coïncider deux sommets :
Avec cette méthode vous pouvez avoir la chance de voir apparaître un lapin parmi les feuilles d’automne ou une colombe d’entre les étoiles.

• Voici ceux de l'Inaccessible Étoile : :
• Voici le polygone de base et le pavé de base du "lapin parmi les feuilles d'automne" :


Vous avez peut-être remarqué que la colombe et l’étoile ci-dessus n’ont pas tout à fait le même contour que la colombe du bas et que l’étoile du haut du dessin. C’est que ce dessin style apparition/disparition cher à escher permet ces à-peu-près. Ces derniers sont parfois encore plus accentués dans les dessins qui vont suivre.

Voici le pavé de base de 'Deux éléments' :
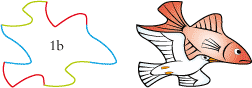
• Cet oiseau et ce poisson auraient été parfaits dans un dessin de style apparition/disparition, mais le résultat aurait alors été trop proche de L’Air et l’Eau d’escher.
• Voici le pavé de base de Regard d’enfant :
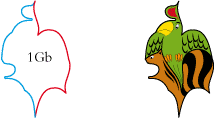
Ce regard d’enfant qui pourrait être celui d’Albert Flocon - ce brillant artiste graveur - qui établit les règles de la perspective curviligne, celle-ci donnant une image plus logique et plus excitante que la perspective classique pour laquelle on a structuré l’espace avec des droites qui le rendent triste.
"Apprise depuis l’enfance, familière depuis quatre siècles,
l’image traditionnelle passe finalement pour l’image vraie.
Ce n’est peut-être qu’une imposture…"
Albert FLOCON / André BARRE
La Perspective curviligne
Et si, maintenant, nous divisions quelques pavés en plusieurs lézards :
• Voici tout d’abord le pavé de base de Lézards au carré, divisé en trois lézards dont deux identiques :


• Et voici celui du pavage ci-contre :

• La Rosace aux lézards est construite à l’aide de pavés du type 4a et 6b entre lesquels on a fait quelques adaptations :
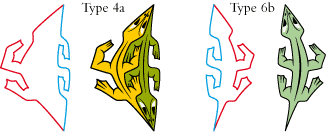

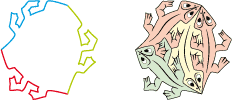
• Le dessin ci-dessous a un pavé de base du type 3b divisé en quatre lézards :

7 PAVER AVEC DES MOTS
Les mots sont la menue monnaie de la pensée.
Il y a des bavards qui nous payent en pièces de dix sous.
D’autres, au contraire, ne donnent que des louis d’or.
Jules RENARD
L’art est beau quand la main, la tête et le cœur travaillent ensemble.
John RUSKIN
 osons-nous la question : les motifs pourraient-ils être autre chose
que des figures familières comme des animaux, des objets ou bien des humains tout en ayant des contours bien reconnaissables ? Eh oui, bien sûr ! il y a les caractères ; ces signes que les hommes
ont imaginé pour communiquer et qui sont, de plus, déjà en deux dimensions.
osons-nous la question : les motifs pourraient-ils être autre chose
que des figures familières comme des animaux, des objets ou bien des humains tout en ayant des contours bien reconnaissables ? Eh oui, bien sûr ! il y a les caractères ; ces signes que les hommes
ont imaginé pour communiquer et qui sont, de plus, déjà en deux dimensions.Et mieux encore : il y a les ensembles de caractères que sont les mots et qui ont une signification bien précise. Nous pouvons choisir un mot pour ce ou celui qu’il représente, pour sa valeur à nos yeux. Nous pouvons le dessiner, le travailler, le parfaire … l’aimer tout autant qu’un poète.
Pourquoi escher n’a t-il pas fait de pavages avec des mots reste un grand mystère. La voie a été indiquée dans un livre de Scott Kim. Son titre ? Inversion. Un livre unique, à la frontère entre la calligraphie et les mathématiques. On y trouve, entre autres merveilles, le mot ‘’figure’’ en blanc sur fond noir et dont l’espace entre les lettres se transforme progressivement en lettres noires sur fond blanc, formant à nouveau le mot ‘’figure’’ en négatif. On y trouve aussi le mot ‘’Lester’’ avec l’espace entre les lettres formant le mot ‘’Pearl’’ (ce sont les parents de Kim). Ce ne sont pas des pavages mais c’est déjà la bonne voie.
Il était tentant d’emprunter cette voie et de faire des mots dans le style de Kim. Il a été enthousiasmant d’aller au bout du chemin et de réaliser un vieux rêve d’enfance : faire des pavages avec des mots. Et si possible avec des mots qui tiennent à cœur.

Nous avons vu qu’il est aisé de diviser un pavé en deux, trois ou plus. Eh bien un mot-pavé n’est jamais que l’équivalent d’un pavé divisé en autant de sous-pavés qu’il comporte de lettres, d’accents et/ou de points sur les i. C’est l’assemblage du pavé de base avec ses transformées puis le coloriage qui permet de lire le mot dans différentes couleurs.
• Il n’y a pas de pavage dans l’exemple ci-contre. Mais on pourrait y tailler des pavés de type 4b comme celui ci-dessous :

• Parmi plusieurs premières tentatives de pavage avec un mot, voici celle-ci à droite :
Tentative non concluante. Mais le résultat est tout de même intéressant.

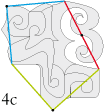
• Honneur au bon maître. Voici le pavé de base type 4c utilisé pour escher pavage :
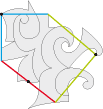
Les transformées de ce pavé de base permettent de lire le mot ‘’escher’’ dans quatre directions.
• On retrouve ce mot-pavé en décor autour du portrait d’escher :
• Reprenons le mot-pavé ‘’escher’’. Et colorions-le comme ci-dessous. Nous voyons alors apparaître … Le Jardin d’escher.
Exemple de carrelage :


• Voici le pavé de base type 2e de Kim :
• Axes de translation, axes de rotation, axes de symétrie, axes de réflexion glissée ; les axes sont présents dans tous les pavages. Voici le pavé de base type 6a d'Axes :
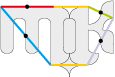
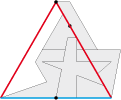
Les transformées de ce pavé de base permettent de lire le mot ‘’Kim’’ dans deux directions.
• En route pour un petit tour dans les "étoiles". Voici le pavé de base type 6a utilisé :
• Puis voici le pavé de base type 2c d'Inversion, un mot particulièrement cher à Scott Kim :

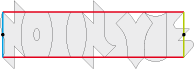
• Honneur à l’ordre naturel, voici le pavé de base type 4c utilisé pour L’Ordre et le Chaos :
• Encore un contraire, voici le pavé de base type 1b de Paradoxe Jour / Nuit :
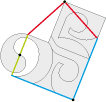
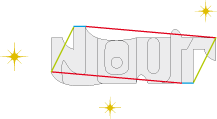
• Bien sûr, il faut un nom de musicien. Citer des génies tels que Bach ou Mozart ferait certainement bonne impression … mais ne refléterait pas mon goût pour la bonne vieille musique Country, musique que j’aime et qui m’apporte joie et satisfaction. Et que l’on ne vienne pas me dire qu’il n’y a pas de génie dans la musique Country. Merle Travis non seulement en était un, mais était, de plus un génie multi-talents. Il excellait à la fois comme auteur, compositeur, caricaturiste, horloger, historien, acteur, écrivain, naturaliste, imitateur, concepteur de guitares, chanteur et bien sûr comme guitariste virtuose. On lui doit le style de guitare qui porte son nom, le Travis-pickin’. Style où l’accompagnement, les basses et la mélodie sont joués en même temps.
Voici le pavé de base de Travis:

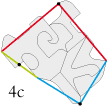

• Brassens… Ah, Brassens ! L’homme aux cent chef-d’œuvres. Le perfectionniste du ‘’beau langage’’ et de l’expression choisie. Le merveilleux artisan ciseleur de mots.
Que le mot ‘’Brassens’’ s’étende à l’infini.

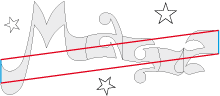
• Suivant qu’elle est blanche ou noire, la magie désigne soit l’art de produire certains effets merveilleux qui ne sont dus qu’à des causes naturelles,
soit la mystificaton sordide par laquelle certaines personnes ont la prétention de produire des effets surnaturels par l’intervention des esprits.
Voici le pavé de base type 1a utilisé dans Magie blanche / Magie noire :
• Parmis les artistes de la magie blanche, Gérard Majax en est un digne représentant, lequel n’hésite pas à œuvrer contre les fumistes de l’illusion,
les soi-disant possesseurs de pouvoirs extraordinaires et autres ‘’tordeurs‘’ de petites cuillères.
Voici son pavé de base type 1b :
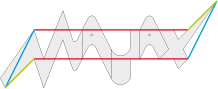
• Naturellement, voici le pavé de base type 1b de l’incon-tournable Infini :
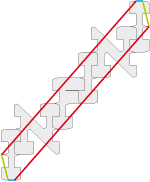
• Puis voici le pavé de base type 2e de Pavé ! D'abord en deux tons puis en un seul ton dégradé.

• Ce pavé type 6a presque triangulaire est celui de Pavage victorien :
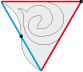
• Si un nom mérite bien de paver l’infini, c’est bien celui d’"Einstein". Voici le pavé de base type 2e utilisé :

"La joie de contempler et de comprendre,
voilà le language que me porte la nature."
Albert EINSTEIN
Comment je vois le monde
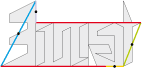
• Erno Rubik est l’inventeur du Rubik’s Cube, le plus diabolique de tous les casse-têtes. Voici le pavé de base type 6d de Rubik's Cube :
• Où se situe la frontière entre le bien et le mal ? Voici le pavé de base type 1b de Frontière :
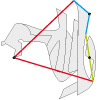
• Voici celui de Nicolas Pavage 2 en type 3a :
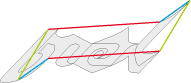
• Il est, bien sûr, tentant de paver avec son propre nom. Voici le pavé de base type 1b de Nicolas :
• Pour finir avec les mots, revoici ‘’infini’’ écrit de façon qu’avec sa transformée par rotation il occupe exactement un rectangle. On peut alors assembler les mots comme des briques.
• Puis le même mot dans un parallélogramme :


8 DÉFORMER LES CANEVAS
Ce qui vaut la peine d’être fait vaut la peine d’être bien fait.
Nicolas POUSSIN
L’harmonie des proportions satisfait les sens.
Saint Thomas d'AQUIN
 e mieux est l’ennemi du bien. Mais le bien
est souvent l’ami du médiocre ! Cherchons le mieux en déformant les canevas pour en habiller des cercles concentriques, des spirales, des effets de perspective ou de
volume. Cela nous permettra de découvrir de nouveaux horizons pleins de merveilleuses harmonies.
e mieux est l’ennemi du bien. Mais le bien
est souvent l’ami du médiocre ! Cherchons le mieux en déformant les canevas pour en habiller des cercles concentriques, des spirales, des effets de perspective ou de
volume. Cela nous permettra de découvrir de nouveaux horizons pleins de merveilleuses harmonies.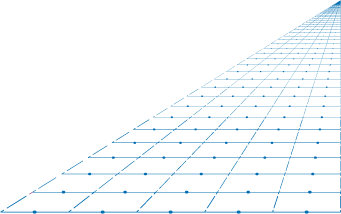

Ci-contre, voici par exemple ce que donne un canevas du type 2S sur une perspective :

• Voici le pavage type 2Gb de Cascade :
• Voici celui de Miel, type 2Sb :


• Voici celui de Plouf ! type 1Sb :
• Voici celui de Spirale d'infini, type 2d :

Salut…
C'est encore
moi !
• Ci-contre, voici le pavage d’origine type 6b qui a servi pour Cercles. Neuf couleurs sont nécessaires pour avoir des cercles de lézards ne se coupant pas.

• Ce même pavage a également servi pour l’Icosaèdre aux lézards ci-dessous. Un icosaèdre est un polyèdre avec vingt triangles équilatéraux pour faces. Six couleurs
sont nécessaires pour avoir une répartition harmonieuse. Il y a cinq nez de lézards par sommet.
• Comment mettre sept nez de lézards par sommet ? C’est impossible sur le plan normal, mais pas sur un disque hyperbolique. Les lézards se trouvent alors diminués jusqu’à l’infini sur une limite circulaire. Pour que les lézards qui se suivent soient de la même couleur et que deux colonnes de même couleur ne se croisent pas, sept couleurs sont nécessaires. En fait, dans tout le disque, si l’on tient compte des couleurs, il n’y a pas deux lézards identiques.

9 JOUER AVEC LES ISOMÉTRIES
C’est faire confiance à la vie,
que se mesurer avec l’impossible.
Panait ISTRATI
Atteindre l'inaccessible étoile, telle est ma quête.
Jacques BREL
 n ne peut aller au-delà des limites du
possible, mais on peut les reculer. Pour cela, que pouvons-nous encore faire ? Par exemple, aurions-nous la possibilité de modifier ou de rajouter des isométries sur les
polygones de base ? La réponse est oui. Nous obtenons alors des super-pavés aux caractéristiques étonnantes.
n ne peut aller au-delà des limites du
possible, mais on peut les reculer. Pour cela, que pouvons-nous encore faire ? Par exemple, aurions-nous la possibilité de modifier ou de rajouter des isométries sur les
polygones de base ? La réponse est oui. Nous obtenons alors des super-pavés aux caractéristiques étonnantes.
• Prenons le polygone de base 3a :
Ajoutons-lui les isométries du polygone de base 1Gb, soit deux réflexions glissées. Nous obtenons alors le polygone suivant :
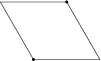
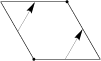
Sur un losange nous avons deux isométries différentes de rotation 3.
Dessinons un motif selon ce polygone. Par exemple le ‘’p’tit loup’’ ci-contre. Il a l’air effaré car il vient de se rendre compte qu’il pouvait paver le plan
non seulement selon les types 3a et 1Gb, mais également de bien d’autres façons.

Pavage type 3a :
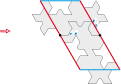
Pavé type 2c divisé en deux motifs identiques

Pavé type 2Ge divisé en deux motifs identiques
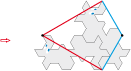
Pavé type 6c divisé en deux motifs identiques
Pavage type 1Gb :

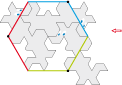
Pavé type 3b divisé en trois motifs identiques
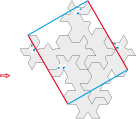
Pavé type 1a divisé en quatre motifs identiques
• Prenons maintenant le polygone de base 6a. Nous avons là un triangle équilatéral possédant une isométrie de rotation 6 et une de rotation 2 :
Par exemple ce poisson :

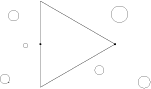
De ce poisson, nous pouvons, bien sûr, faire un pavage de type 6a :

Puis dessinons un motif de façon que chaque côté de la rotation 2 soit la réduction de moitié de chaque déformation compensée de la rotation 6 :
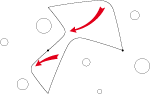

Mais nous pouvons aussi lui accoler trois petits poissons identiques :
De cette façon, cela nous donne un pavé de type 6d divisé en quatre :
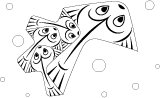
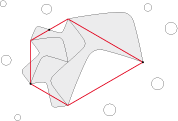
Mais ce n’est pas tout. Reprenons notre poisson et faisons lui subir une rotation 6. Nous pouvons rajouter tout autour une couronne de petits poissons. Puis à nouveau, accoler une couronne de poissons encore plus petits, et ainsi de suite jusqu’à l’infini. Nous obtenons alors une figure parfaitement hexagonale.
• Non sans rappeler l’exemple précédent, mais avec un résultat différent, prenons un cerf-volant du type 6c :
Pavage type 6c :

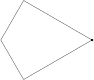
Dessinons un motif de façon que les deux côtés de la rotation 3 soient égaux aux côtés de la rotation 6 par la tangente de 30° (0,5774). Par exemple ce papillon :
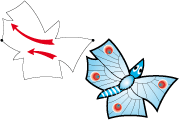
Pavage type 6d :
Nous pouvons faire un pavage de type 6c mais également de type 6d si nous accolons quatre petits papillons comme ci-dessous :
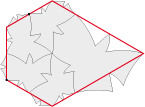
Pour construire le Flocon de papillon ci-dessous, il faut faire une rotation 6. Puis à la périphérie, accoler une couronne de petits papillons quatre fois plus
nombreux. Puis à cette nouvelle périphérie, faire de même trois fois.
On peut, bien entendu, continuer de rajouter des couronnes à l’infini. Chaque nouvelle couronne
alors, générera de plus en plus de points d’infini comme ci-dessous. En sommes nous obtiendrons… une infinité d’infinis.
• Comme pour le papillon, mais en inversant les côtés de la rotation 3, nous pouvons faire l'oiseau ci-contre.
Le voici ci-dessous en se limitant à la cinquième couronne.
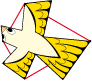
• Prenons le polygone de base 4S, soit un carré ayant deux rotations 4 symétriques. Puis rajoutons-lui quatre rotations 2 :
Dessinons, par exemple, cet oiseau :

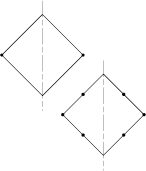
Nous pouvons paver le plan selon différents types ou bien faire une rosace ou un pavage non périodique tel celui ci-dessous. L’on y voit une masse grouillante d’oiseaux parmis lesquels certains vont droit leur chemin et quelques-uns, plus rares, illuminent les quatres horizons.
• Voyons si nous pouvons dessiner un motif qui possède plusieurs pavés de base :
Ce ‘’brav’ toutou’’ fera l’affaire :

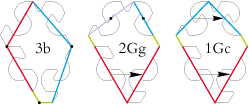
Pavage type 3b :
Pavage type 2Gg :
Pavage type 1Gc :
Rosace :



• Et si nous retrouvions nos amis les lézards ? Dans l’estampe De plus en plus petit (N°35), escher a utilisé un triangle rectangle isocèle du type 4a pour diminuer ses lézards jusqu’à l’infini selon le shéma ci-dessous :
Cela nous permet de dessiner deux lézards par triangle au lieu d’un :
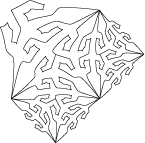
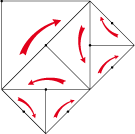
Nous pouvons maintenant faire une rotation 4 et diminuer les lézards jusqu’à l’infini. La façon la plus directe donne un
octogone.
En fait, il n’y a pas qu’un couple de lézards différents, mais quatre. Cela afin de permettre les adaptations.
escher,
dans De plus en plus petit, a dessiné neuf lézards différents.
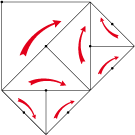
Inversons le sens
des triangles comme suit :
J’espère que vous avez eu beaucoup de plaisir à regarder cette méthode. Ce sera le mot de la…
Retourner au sommaire
Nota bene :
Si cette méthode vous a plu,
un petit mot dans le "Livre d'or"
me ferait plaisir.
















































































 NICOLAS 2014
NICOLAS 2014
