Rosace pentagonale aux oiseaux 
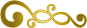
Pavés apériodiques Penrose P2
De tous les ensembles remarquables de polygones apériodiques, il semble que seuls 7 permettent la construction de pavages figuratifs.
Pour cela, les cotés des polygones doivent subir des déformations symétriques, rotatoires ou quelconques, et la forme obtenue des pavés doit suffire à elle seule à constituer un pavage apériodique sans la nécessité de signes,
de lignes ou de chiffres. Ces pavés sont extraordinaires. Prenons par exemple les pavages de Penrose P2 et P3. Si vous ne suivez pas les lignes dessinées dessus, il deviennent périodiques, mais si vous déformez leurs bords,
qu’il y aient des lignes ou pas dessus, vous ne pourrez construire que des pavages apériodiques.
On peux dire que certains des pavés de Robert Ammann pourraient également en faire partie, mais des bords rectilignes ou des clefs nécessaires rendent illusoire de faire toute forme figurative.
Voici un des deux plus célèbre pavages apériodiques. C’est le pavage de Roger Penrose nommé P2 découvert en 1977. C’est un pavage d’ordre 5 comme le P1 ou le P3. C’est ma première tentative de rendre figuratif un pavage
apériodique. Les étoiles correspondent au points de rencontre des pavés si on les continuait.
NICOLAS 2014
